В апреле в издательстве МИФ выходит книга кандидата физико-математических наук Сергея Самойленко «Вероятности и неприятности. Математика повседневной жизни». Автор на житейских примерах объясняет, как работают законы подлости. «Москвич Mag» публикует фрагмент о том, почему дожди постоянно выпадают на выходные.

Так правда ли, что дожди предпочитают выходные дни?

В начале главы мы говорили о том, что выходные и непогода совпадают чаще, чем хотелось бы. Попробуем завершить это исследование.

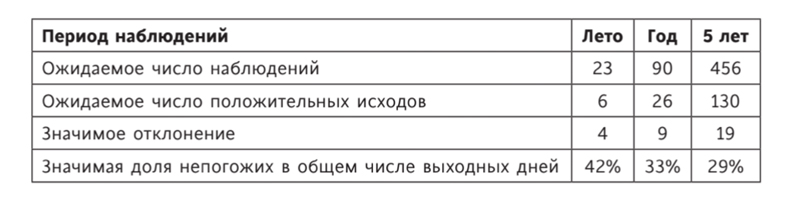
Каждый дождливый день можно рассматривать как наблюдение случайной величины — дня недели, подчиняющегося распределению Бернулли с вероятностью 1/7. Примем в качестве нулевой гипотезы предположение, что все дни недели одинаковы с точки зрения погоды и дождь может пойти в любой из них равновероятно. Выходных у нас два, итого получаем ожидаемую вероятность совпадения непогожего дня и выходного равной 2/7. Эта величина будет параметром распределения Бернулли. Как часто идет дождь? В разное время года по-разному, конечно, но в Петропавловске-Камчатском в среднем наблюдается девяносто дождливых или снежных дней в году. Так что доля дней с осадками составляет около 90/365 ≈ 1/4. Предположим на основании этого, что в течение некоторого периода (месяц, полгода, год) в среднем 1/4 дней окажутся непогожими. Посчитаем, какое количество дождливых выходных мы должны зарегистрировать, чтобы быть уверенными в том, что существует некоторая закономерность. Результаты приведены в таблице.

О чем говорят эти цифры? Если вам кажется, что который год подряд «лета не было», злой рок преследует ваши выходные, насылая на них дождь, это можно проверить и подтвердить. Однако в течение лета уличить злой рок можно, лишь если больше двух пятых выходных окажутся дождливыми. Нулевая же гипотеза предполагает, что только четверть выходных должна совпасть с ненастной погодой. За пять лет наблюдений уже можно надеяться подметить тонкие отклонения, выходящие за пределы 5%, и при необходимости приступать к их объяснению.

Я воспользовался школьным дневником погоды, который велся с 2014 по 2018 год, и выяснил, что за эти пять лет было 459 ненастных дней, из которых 141 пришелся на выходные. Это действительно больше ожидаемого числа на 11 дней, но значимые отклонения начинаются с 19 дней, так что это, как мы говорили в детстве, «не считается».

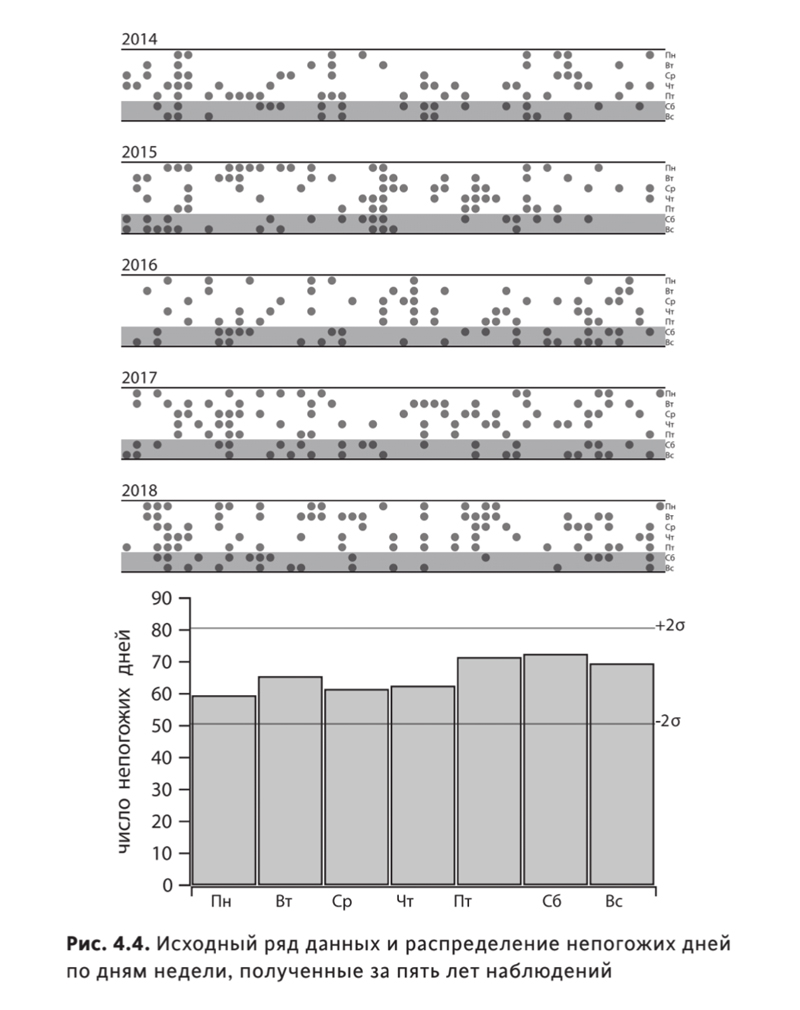
Вот как выглядят ряд данных и гистограмма, показывающая распределение непогоды по дням недели. Горизонтальными линиями на ней отмечен интервал, в котором может наблюдаться случайное отклонение от равномерного распределения при том же объеме данных.

Видно, что, начиная с пятницы, действительно наблюдается увеличение числа дней с плохой погодой. Но для поиска причины роста предпосылок недостаточно: такой же результат можно получать, перебирая случайные числа. Вывод: за пять лет наблюдения за погодой я накопил почти две тысячи записей, но ничего нового о распределении погоды по дням недели не узнал.

При взгляде на записи в дневнике явно бросается в глаза, что непогода приходит не отдельными днями, а двух-трехдневными периодами или даже недельными циклонами.

Это как-то влияет на результат? Можно попробовать принять это наблюдение во внимание и предположить, что дожди идут в среднем по два дня (на самом деле 1,7 дня); тогда вероятность перекрыть выходные увеличивается до 3/7. Тогда ожидаемое число совпадений для пяти лет должно составить 195±21, или от 174 до 216 раз. Наблюденная величина 141 не входит в этот диапазон, и, значит, гипотезу об эффекте сдвоенных дней непогоды можно смело отвергать. Узнали ли мы что-то новое? Да: казалось бы, очевидная особенность процесса не влечет никакого эффекта. Об этом стоит поразмыслить, и мы этим займемся чуть позже. Но главный вывод таков: какие-то более тонкие эффекты рассматривать нет резона, поскольку простого объяснения.

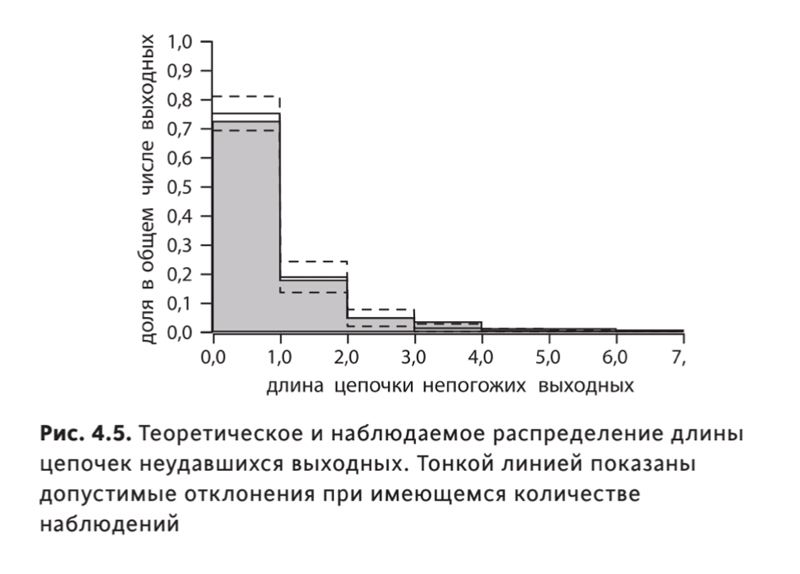
Но недовольство у нас вызывает не пятилетняя и даже не годовая статистика: человеческая память не такая долгая. Обидно, когда дождливые дни выпадают на выходные три или четыре раза подряд! Как часто это может случаться? Особенно если вспомнить, что гадкая погода не приходит одна. Задачу можно сформулировать так: «Какова вероятность того, что n выходных подряд окажутся дождливыми?» В главе 6 мы близко познакомимся с так называемыми случайными процессами как с моделями случайных последовательностей событий во времени. Один из них, особенно важный и вместе с тем особенно простой, называется пуассоновским. Его характерная особенность — независимость момента наступления следующего события от предыдущих, уже произошедших, а также то, что временны ́е интервалы между событиями подчиняются экспоненциальному распределению. Такая последовательность характеризуется одним параметром, который называют интенсивностью: числом событий, в среднем случающихся за единичный интервал времени. Разумно предположить, что непогожие дни образуют пуассоновский поток с интенсивностью 1/4. Это полностью соответствует нашему исходному положению, что в среднем четверть дней любого периода будет непогожей. Если рассматривать только выходные, процесс не должен изменить интенсивность, и из всех выходных непогожие дни должны составлять в среднем тоже четверть. Итак, выдвигаем нулевую гипотезу: ненастья формируют последовательность согласно пуассоновскому процессу с известным параметром, а значит, интервалы между пуассоновскими событиями описываются экспоненциальным распределением. Нас интересуют дискретные интервалы: 0, 1, 2, 3 дня и т. д., — поэтому мы можем воспользоваться дискретным аналогом экспоненциального распределения — геометрическим распределением с параметром 1/4. На рисунке 4.5 показано, что у нас получилось. Очевидно: предположение о том, что мы наблюдаем пуассоновский процесс, нет резона отвергать.

Можно задаться таким вопросом: сколько лет нужно вести наблюдения, чтобы замеченную нами разницу в 11 дней можно было бы уверенно подтвердить или отвергнуть как случайное отклонение? Это легко посчитать: наблюдаемая вероятность 141/459 = 0,307 отличается от ожидаемой 2/7 = 0,286 на 0,02. Для фиксации различия в сотых требуется абсолютная погрешность, не превышающая 0,005, что составляет 1,75% от измеряемой величины. Отсюда получаем необходимый объем выборки n ≥ (4∙5/7)/(0,01752∙2/7) ≈ 32 000 дождливых дней. Это потребует около 4∙32000/365 ≈ 360 лет непрерывных метеорологических наблюдений, ведь только каждый четвертый день идет дождь или снег. Увы, данных за такой срок нет. Это даже больше, чем время, которое Камчатка находится в составе России, поэтому шансов выяснить, как обстоят дела «на самом деле», у меня нет. Особенно если учесть, что за это время климат успел измениться разительно — из малого ледникового периода природа выходит в очередной оптимум.

Как же австралийским исследователям удалось зафиксировать отклонение температуры в доли градуса и почему имеет смысл всерьез рассматривать это исследование? Дело в том, что они использовали часовые данные температуры, которые не были «прорежены» каким-либо случайным процессом. Таким образом, за 30 лет метеонаблюдений удалось накопить более четверти миллиона отсчетов с нескольких датчиков, что позволяет уменьшить стандартное отклонение среднего в 500 раз по отношению к стандартному суточному отклонению температуры. Этого вполне достаточно, чтобы говорить о точности в десятые доли градуса. Кроме того, авторы использовали еще один красивый метод, подтверждающий наличие временного цикла: случайное перемешивание временнóго ряда. Такое перемешивание сохраняет статистические свойства, такие как интенсивность потока событий во времени, однако «стирает» временные закономерности, делая процесс истинно пуассоновским.

Сравнение множества синтетических рядов и экспериментального позволяет убедиться в том, что замеченные отклонения процесса от пуассоновского значимы. Таким же образом сейсмолог Александр Гусев показал, что землетрясения в каком-либо районе образуют своеобразный самоподобный поток со свойствами кластеризации*. Это означает, что землетрясения имеют обыкновение группироваться во времени, образуя весьма неприятные уплотнения потока. Позже выяснилось, что последовательность крупных вулканических извержений обладает тем же свойством.

___________________________________

* Gusev A. A. Multiscale order grouping in sequences of Earth’s earthquakes // Izvestiya, Phys. Solid Earth. 2005. Vol. 41. Pp. 798–812